Array C Programing

Question: What is Sparse Matrix? Explain by giving an example.

Answer:

Sparse Matrix

A matrix is a two-dimensional object with a total of m x n values made up of m rows and n columns. If most of the matrix elements are worth 0, then Its is called sparse matrix.

or,

Matrices with a relatively high proportion of zero entries are called sparse matrices. Two general types of n-square sparse matrices, which occur in various applications, are:

• Tridiagonal Matrix
• Triangular Matrix

 

Triangular Matrix

The  triangular matrix, where all entries where above the main diagonal are zero equivalently where zero entries can only occur on or below the main diagonal is called a lower Triangular Matrix.

 

Tridiagonal Matrix

The matrix, where non-zero entries can only occur on the diagonal or on elements immediately above or below the diagonal is called a Tridiagonal matrix.

 

 

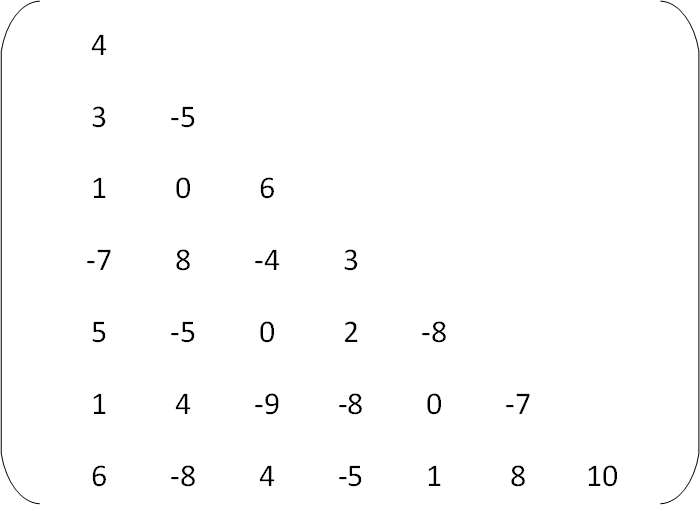
Explain with Example

The natural method of representing matrices in memory as 2-D arrays may not be suitable for sparse matrices. That is, one may save space by storing
only those entries, which may be non-zero. This can be explained with the following example:

 

 

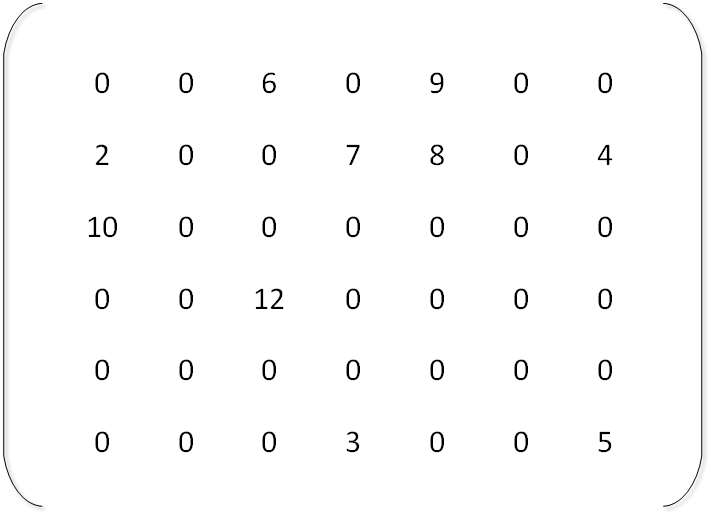
Non-zero element are:

M[1][3] = 6, M[1][5] = 9,

M[2][1] = 2, M[2][4] = 7,

M[2][5] = 8, M[2][7] = 4,

M[3][1] = 10, M[4][3] = 12,

M[6][4] = 3,M[6][4] = 5;

One of the basic methods for storing such, a sparse matrix is to store non-zero elements in a one-dimensional array and to identify each array element with row and column indices as:

 

 

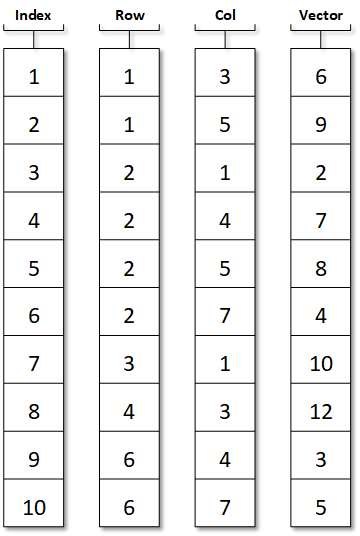
Sequential Representation of Sparse Matrix

The ith element of vector V is the matrix element with row; column indices Row[i] and Col[i].