Array C Programing

Question: Explain Insertion Sort Algorithm and its complexity.

Answer: Insertion Sort Algorithm:-

This algorithm scans an array 'list' (with n element list[1], list [2], .... list[n]) from list [1] to list[n], inserting each element list [i] into its proper position in the previously sorted subarray list[1], list[2],......,list [i-1]. That is:

Pass 1: list [1] by itself is trivially sorted.

Pass 2: list [2] is inserted before or after list[1] so that: list[1], list[2] is sorted.

Pass 3: list [3] is inserted into its proper place in the list[1], list[2], that is before list[1], between list[1] and list[2], or after list[2], so that: list[1], list[2], list[3], list[4] is sorted.

Pass 4: list[4] is inserted into its proper place in list[1], list[2], list[3], so that: list[1], lis[2], list[3], list[4], is sorted. 

Pass n: list [n] is inserted into its proper place in list[1], list[2], ..., list[n-1] so that: list[1], list[2],... list[n-1], is sorted.

This algorithm is frequently using when n is small.

The problem of deciding how to insert list[i] in its proper place in the sorted subarray list[1], list[2],...,list[i-1], can be accomplished by comparing list[i] with list [i-j], comparing list[i] with [i-2], and so on, until first meeting an element list[j] such that list[j] <= list[i].

Then each of the element list[i-1], list[i -2], ..., list[j +1] is moved forward one location, and list[i] is then inserted in the j+1st position in the array. The algorithm is simplified if there always is an element list[j] such that list[j] <= list[i], otherwise, we must constantly check to see if we are comparing list[i] with list[1]. This condition can by accomplished by using a sentinel element list[0] = -∞ (or a very small number).

Example:

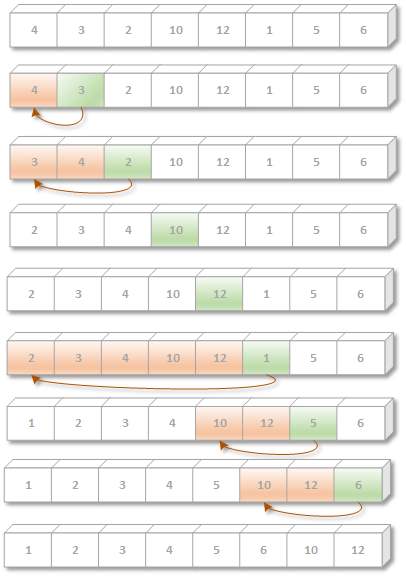
The insertion sort algorithm is given below:

Algorithm: (Insertion sort) INSERTION (list, n)

This algorithm sorts the array list with n elements;

Step 1: set list[0]: =-∞ [Initialises sentinel element]

Step 2: Repeat Step 3 to 5 for i = 1,2,... n

Step 3: set temp: - list[i], and, ptr: = i - 1

Step 4: Repeat while temp < list[ptr]

(a) set list[ptr + 1]: = list[ptr] [moves element forward]

(b) set ptr: = ptr -1 [End of loop]

Step 5: set list[ptr + 1]: = temp [Inserts element in proper place] [End of Step 2 loop]

Step 6: Return

Complexity of Insertion Sort:

The worst case occurs when the array 'list' is in reverse order and inner loop must use the maximum number i-1 of comparisons.

Hence, total comparisons are :
f(n) = 1 + 2 + 3 +.....+ (n - 1) =n(n-1)/2=O(n²)

In the average case there will be approximately (i - 1)/2 comparisons in the inner loop.

Hence f(n)=1/2+2/2+.....+n-1/2=n(n-1)/4=O(n²)

Thus, it is  a very slow algorithm when n is very large.